
이 포스팅에서 작성하는 내용은 이것이 취업을 위한 코딩테스트다 (나동빈 지음) 에서 발췌하였습니다.
(원본 소스코드 : https://github.com/ndb796/python-for-coding-test/)
1. 이전에 공부했던 그래프 복습
1) 그래프(Graph) : 노드와 노드 사이에 연결된 간선 정보를 가지는 자료구조
(서로 다른 개체가 연결 or 여러 도시가 연결 과 같은 경우는 그래프 알고리즘 의심)
- 다익스트라 알고리즘 : 시작점에서부터 다른 각각의 노드로 가는 최단 경로를 구하는 알고리즘. (우선순위 큐를 이용하면 효율적)
- 워셜-플로이드 알고리즘 : 모든 노드에서 각각의 다른 노드까지 최단 경로를 구하는 알고리즘. (인접 행렬을 이용, 노드의 갯수가 적으면 유용)
- 그래프 표현 방법
인접 행렬 : 2차원 배열을 사용하여 그래프 표현
인접 리스트 : 리스트를 사용하는 방식
2) 그래프 vs 트리
| 그래프 | 트리 | |
| 방향성 | 방향 그래프 혹은 무방향 그래프 | 방향 그래프 |
| 순환성 | 순환 및 비순환 | 비순환 |
| 루트 노드 존재 여부 | X | O |
| 노드 간 관계성 | X | O |
| 모델의 종류 | 네트워크 모델 | 계층 모델 |
2. 서로소 집합(Disjoint Sets)
- 공통 원소가 없는 두 집합
ex1 ) {1, 3}, {4, 6} → 서로소 관계이다.
ex2 ) {1, 3}, {3, 6} → 서로소 관계가 아니다. (3이라는 원소가 공통적으로 포함)
1) 서로소 집합 자료구조(union-find합치기 찾기): 서로소 부분 집합들로 나누어진 원소들의 데이터를 처리하기 위한 자료구조
- union과 find 이 2개의 연산으로 조작
- union(합집합) : 2개의 원소가 포함된 집합을 하나의 집합으로 합치는 연산
- find(찾기) : 특정한 원소가 속한 집합이 어떤 집합인 지 알려주는 연산
- 트리 자료구조를 이용해 표현
- 서로소 집합을 그림으로 표현 시, 번호가 큰 노드가 번호가 작은 노드를 간선으로 가리키도록 한다.
import java.util.Scanner;
public class Main {
// V : 노드의 갯수
// M : 간선의 갯수
public static int V, M;
// 노드의 개수는 최대 100,000개라고 가정
// 부모 노드 테이블
public static int[] parent = new int[100001];
// 특정 원소가 속한 집합을 찾기
public static int findParent(int x) {
// 노드의 부모노드가 루트 노드일 경우,
if (x == parent[x]) {
// 반환
return x;
}
// 아니라면, 루트 노드를 찾을 때까지 재귀적으로 호출
return findParent(parent[x]);
}
// 두 원소가 속한 집합을 합치기
public static void unionParent(int a, int b) {
a = findParent(a);
b = findParent(b);
if (a < b) parent[b] = a;
else parent[a] = b;
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
V = sc.nextInt();
M = sc.nextInt();
// 부모 테이블에서, 부모 노드를 자신으로 초기화
for (int i = 1; i <= V; i++) {
parent[i] = i;
}
// Union 연산 수행
for (int i = 0; i < M; i++) {
int a = sc.nextInt();
int b = sc.nextInt();
unionParent(a, b);
}
// 각 원소가 속한 집합 출력하기
System.out.print("각 원소가 속한 집합 : ");
for (int i = 1; i <= V; i++) {
System.out.print(findParent(i) + " ");
}
System.out.println();
// 부모 테이블 내용 출력하기
System.out.print("부모 테이블: ");
for (int i = 1; i <= V; i++) {
System.out.print(parent[i] + " ");
}
System.out.println();
}
}
- 위의 소스코드는 최악의 경우 부모 노드를 확인하는 데 모든 노드를 확인할 수도 있다.
아래의 표 처럼 5번 노드의 루트 노드를 확인하는데 4>3>2>1>1을 확인하게 된다.
| 노드 번호 | 1 | 2 | 3 | 4 | 5 |
| 부모 노드 번호 | 1 | 1 | 2 | 3 | 4 |
- 위의 경우 경로 압축 기법을 적용하여 시간 복잡도를 개선시킬 수 있다.
2) 경로 압축(path Compression) : find 함수를 재귀적으로 호출한 뒤에 부모 테이블을 갱신하는 기법
- 위의 소스코드에서 findParent 함수를 아래 코드와 같이 수정하여 경로압축 기법을 사용한다.
public static int findParent(int x) {
// x의 부모노드가 루트노드일 경우 x 반환
if (x == parent[x]){
return x;
}
// 아니면 루트노드 찾은 후에 parent 배열에 넣고 반환
return parent[x] = findParent(parent[x]);
}
3) 서로소 집합을 활용한 사이클 판별
- 서로소 집합은 무방향 그래프 내에서의 사이클을 판별할 때 사용할 수 있다.
- union연산은 그래프에서의 간선으료 표현될 수 있으며, 간선을 하나씩 확인하면서 두 노드가 포함되어 있는 집합을 합치는 과정을 반복하면 사이클 판별 가능
- 각 간선을 확인하며 두 노드의 루트 노드 확인
- 루트 노드가 서로 다르다면 두 노드에 대해 union 연산 진행
- 루트 노드가 서로 같다면 사이클(Cycle)인 것으로 확인
- 그래프에 포함되어 있는 모든 간선에 대하여 1번의 과정 반복
import java.util.*;
public class Main {
// V : 노드의 갯수
// M : 간선의 갯수
public static int V, M;
public static int[] parent = new int[100001]; // 부모 테이블 초기화하기
// 특정 원소가 속한 집합을 찾기
public static int findParent(int x) {
// x가 루트노드 일 경우 x 반환
if (x == parent[x]) {
return x;
}
// 아닐 경우, 루트노드를 찾기위해 재귀 호출 후 이 값을 반환 및 parent 배열에 저장
return parent[x] = findParent(parent[x]);
}
// 두 원소가 속한 집합을 합치기
public static void unionParent(int a, int b) {
a = findParent(a);
b = findParent(b);
if (a < b) parent[b] = a;
else parent[a] = b;
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
V = sc.nextInt();
M = sc.nextInt();
// 부모 테이블상에서, 부모를 자기 자신으로 초기화
for (int i = 1; i <= V; i++) {
parent[i] = i;
}
boolean cycle = false; // 사이클 발생 여부
for (int i = 0; i < M; i++) {
int a = sc.nextInt();
int b = sc.nextInt();
// 사이클이 발생한 경우 종료
if (findParent(a) == findParent(b)) {
cycle = true;
break;
}
// 사이클이 발생하지 않았다면 합집합(Union) 연산 수행
else {
unionParent(a, b);
}
}
if (cycle) {
System.out.println("사이클 있음");
}
else {
System.out.println("사이클 없음");
}
}
}| 입력 | 출력 |
| 3 3 1 2 2 1 2 3 |
사이클 있음 |
3. 신장 트리
1) 신장 트리(Spanning Tree)
- 하나의 그래프가 있을 때 모든 노드를 포함하면서 사이클이 존재하지 않는 부분 그래프
2) 크루스칼 알고리즘(Kruskal Algorithm)
- 신장 트리 중에서 최소 비용으로 만들 수 있는 트리를 찾는 알고리즘 (최소 신장 트리 알고리즘)
- 그리디 알고리즘으로 분류
- 가장 거리가 짧은 간선부터 차례대로 집합에 추가하는 방식
- 간선의 갯수 = 노드의 갯수 -1
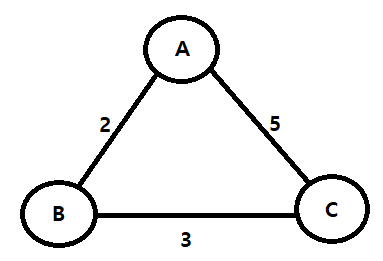
ex) 위의 A, B, C 가 모두 연결되기 위한 최소의 비용(최소 신장 트리)은 아래와 같다.
▶ 2+3 (최소 비용)
▶ 3+5
▶ 2+5
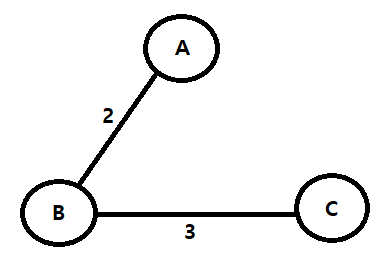
3) 크루스칼 알고리즘 동작 과정
- 간선 데이터를 비용에 따라 오름차순 정렬
- 간선을 하나씩 확인하며 현재의 간선이 사이클을 발생시키는 지 확인
- 사이클 발생 시, 최소 신장 트리에 포함 X
- 사이클 발생 하지 않는 경우, 최소 신장 트리에 포함
- 모든 간선에 대하여 2번 과정을 반복
import java.util.ArrayList;
import java.util.Collections;
import java.util.Scanner;
public class Main {
// Edge 클래스 선언
public static class Edge implements Comparable<Edge>{
private int nodeA;
private int nodeB;
private int distance;
public Edge(int nodeA, int nodeB, int distance) {
this.nodeA = nodeA;
this.nodeB = nodeB;
this.distance = distance;
}
public int getNodeA() {
return nodeA;
}
public int getNodeB() {
return nodeB;
}
public int getDistance() {
return distance;
}
// 우선순위 큐에서 사용
// 거리가 낮을 수록 높은 우선순위를 가짐
@Override
public int compareTo(Edge other) {
if(this.distance < other.distance)
return -1;
else
return 1;
}
}
// V : 노드의 갯수(최대 100000개로 가정)
// M : 간선의 갯수
public static int V, M;
// 부모 테이블
public static int[] parent = new int[100001];
// 그래프를 저장할 변수
public static ArrayList<Edge> graph = new ArrayList<>();
// 결과를 저장할 변수
public static int result = 0;
// 특정 원소의 루트 노드 찾기
public static int findParent(int x) {
// x가 루트노드라면 반환
if (x == parent[x])
return x;
// 아니라면 parent[x]가 루트노드가 될 때까지 재귀호출
return parent[x] = findParent(parent[x]);
}
// 두 원소가 속한 루트 노드를 합치기
public static void unionParent(int a, int b) {
a = findParent(a);
b = findParent(b);
// 큰 수가 작은 수를 바라보도록
if (a < b)
parent[b] = a;
else parent[a] = b;
}
public static void main(String[] args) {
// TODO Auto-generated method stub
Scanner sc = new Scanner(System.in);
V = sc.nextInt();
M = sc.nextInt();
// 부모 테이블에서, 부모를 자기 자신으로 초기화
// 0번 노드는 없다고 가정
for (int i = 1; i <= V; i++) {
parent[i] = i;
}
// 모든 간선에 대한 정보를 입력 받기
for (int i = 0; i < M; i++) {
int a = sc.nextInt();
int b = sc.nextInt();
int cost = sc.nextInt();
graph.add(new Edge(a, b, cost));
}
// 간선을 비용순으로 정렬
Collections.sort(graph);
// 간선을 하나씩 확인하며
for (int i = 0; i < graph.size(); i++) {
int cost = graph.get(i).getDistance();
int a = graph.get(i).getNodeA();
int b = graph.get(i).getNodeB();
// 사이클이 발생하지 않는 경우에만 최소 신장 트리에 포함
// 사이클이 발생하지 않는다 = a와 b의 루트 노드가 같지 않다
if (findParent(a) != findParent(b)) {
unionParent(a, b);
result += cost;
}
}
// 결과 출력
System.out.println(result);
}
}
4. 위상 정렬
1) 위상 정렬(Topology Sort) : 순서가 정해져 있는 일련의 작업을 차례대로 수행해야 사용할 수 있는 알고리즘
- 방향 그래프의 모든 노드를 '방향성에 거스르지 않도록 순서대로 나열하는 것'
- 진입차수(Indegree) : 특정한 노드로 들어오는 간선의 개수
2) 위상 정렬의 동작 과정
- 진입차수가 0인 노드를 큐에 넣는다.
- 큐가 빌 때까지 아래의 과정을 반복한다.
- 큐에서 원소를 꺼내 해당 노드에서 출발하는 간선을 그래프에서 제거한다.
- 새롭게 진입차수가 0이 된 노드를 큐에 넣는다.
- 만약, 모든 원소를 방문하기 전에 큐가 비어버리면 사이클이 발생한 것이다. (위상 정렬 문제에서는 사이클이 존재하지 않는다고 명시하는 경우가 많음)
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.Queue;
import java.util.StringTokenizer;
public class Main {
// N : 노드의 갯수
// M : 간선의 갯수
public static int N, M;
// 그래프
public static ArrayList<ArrayList<Integer>> graph = new ArrayList<ArrayList<Integer>>();
// 각 노드 별 진입차수 체크
public static int[] inde;
public static void topologySort() {
Queue<Integer> q = new LinkedList<>();
ArrayList<Integer> result = new ArrayList<>();
// 진입차수가 0인 노드를 큐에 넣기
for(int i=1; i<=N; i++) {
if(inde[i]==0)
q.offer(i);
}
// 큐가 빌 때까지 반복
while(!q.isEmpty()) {
// 큐에서 꺼내고
int now = q.poll();
// 결과 리스트에 넣기
result.add(now);
// 현재 큐에서 이어지는 간선을 빼주기
for(int i=0; i<graph.get(now).size(); i++) {
inde[graph.get(now).get(i)] -= 1;
// 그 때, 진입차수가 0이면 큐에 넣기
if(inde[graph.get(now).get(i)] == 0)
q.offer(graph.get(now).get(i));
}
}
System.out.print("순서 : ");
// 결과 출력
for(int i=0;i<result.size();i++) {
System.out.print(result.get(i)+" ");
}
}
public static void main(String[] args) throws IOException {
// TODO Auto-generated method stub
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
// 노드의 갯수와 간선의 갯수 입력받기
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
// 진입차수 배열 크기 할당
inde = new int[N+1];
// 그래프 설정
for(int i=0;i<N+1; i++) {
graph.add(new ArrayList<Integer>());
}
for(int i=0; i<M; i++) {
st = new StringTokenizer(br.readLine());
int from = Integer.parseInt(st.nextToken());
int to = Integer.parseInt(st.nextToken());
graph.get(from).add(to);
// 진입차수 설정
inde[to] += 1;
}
// 위상정렬 호출
topologySort();
}
}| 입력 | 출력 |
| 7 8 1 2 1 5 2 3 2 6 3 4 4 7 5 6 6 4 |
순서 : 1 2 5 3 6 4 7 |
'Algorithm' 카테고리의 다른 글
| [이것이 코딩테스트다] 9. 그래프 - 실전 문제 풀이 (0) | 2022.02.12 |
|---|---|
| [BAEKJOON] 2665번 : 미로만들기 (JAVA) (0) | 2022.02.11 |
| [BAEKJOON] 4485번 : 녹색 옷 입은 애가 젤다지? (JAVA) (0) | 2022.02.08 |
| [BAEKJOON] 13549번 : 숨바꼭질 3 (JAVA) (0) | 2022.02.07 |
| [BAEKJOON] 1916번 : 최소 비용 구하기 (JAVA) (0) | 2022.02.04 |

이 포스팅에서 작성하는 내용은 이것이 취업을 위한 코딩테스트다 (나동빈 지음) 에서 발췌하였습니다.
(원본 소스코드 : https://github.com/ndb796/python-for-coding-test/)
1. 이전에 공부했던 그래프 복습
1) 그래프(Graph) : 노드와 노드 사이에 연결된 간선 정보를 가지는 자료구조
(서로 다른 개체가 연결 or 여러 도시가 연결 과 같은 경우는 그래프 알고리즘 의심)
- 다익스트라 알고리즘 : 시작점에서부터 다른 각각의 노드로 가는 최단 경로를 구하는 알고리즘. (우선순위 큐를 이용하면 효율적)
- 워셜-플로이드 알고리즘 : 모든 노드에서 각각의 다른 노드까지 최단 경로를 구하는 알고리즘. (인접 행렬을 이용, 노드의 갯수가 적으면 유용)
- 그래프 표현 방법
인접 행렬 : 2차원 배열을 사용하여 그래프 표현
인접 리스트 : 리스트를 사용하는 방식
2) 그래프 vs 트리
| 그래프 | 트리 | |
| 방향성 | 방향 그래프 혹은 무방향 그래프 | 방향 그래프 |
| 순환성 | 순환 및 비순환 | 비순환 |
| 루트 노드 존재 여부 | X | O |
| 노드 간 관계성 | X | O |
| 모델의 종류 | 네트워크 모델 | 계층 모델 |
2. 서로소 집합(Disjoint Sets)
- 공통 원소가 없는 두 집합
ex1 ) {1, 3}, {4, 6} → 서로소 관계이다.
ex2 ) {1, 3}, {3, 6} → 서로소 관계가 아니다. (3이라는 원소가 공통적으로 포함)
1) 서로소 집합 자료구조(union-find합치기 찾기): 서로소 부분 집합들로 나누어진 원소들의 데이터를 처리하기 위한 자료구조
- union과 find 이 2개의 연산으로 조작
- union(합집합) : 2개의 원소가 포함된 집합을 하나의 집합으로 합치는 연산
- find(찾기) : 특정한 원소가 속한 집합이 어떤 집합인 지 알려주는 연산
- 트리 자료구조를 이용해 표현
- 서로소 집합을 그림으로 표현 시, 번호가 큰 노드가 번호가 작은 노드를 간선으로 가리키도록 한다.
import java.util.Scanner;
public class Main {
// V : 노드의 갯수
// M : 간선의 갯수
public static int V, M;
// 노드의 개수는 최대 100,000개라고 가정
// 부모 노드 테이블
public static int[] parent = new int[100001];
// 특정 원소가 속한 집합을 찾기
public static int findParent(int x) {
// 노드의 부모노드가 루트 노드일 경우,
if (x == parent[x]) {
// 반환
return x;
}
// 아니라면, 루트 노드를 찾을 때까지 재귀적으로 호출
return findParent(parent[x]);
}
// 두 원소가 속한 집합을 합치기
public static void unionParent(int a, int b) {
a = findParent(a);
b = findParent(b);
if (a < b) parent[b] = a;
else parent[a] = b;
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
V = sc.nextInt();
M = sc.nextInt();
// 부모 테이블에서, 부모 노드를 자신으로 초기화
for (int i = 1; i <= V; i++) {
parent[i] = i;
}
// Union 연산 수행
for (int i = 0; i < M; i++) {
int a = sc.nextInt();
int b = sc.nextInt();
unionParent(a, b);
}
// 각 원소가 속한 집합 출력하기
System.out.print("각 원소가 속한 집합 : ");
for (int i = 1; i <= V; i++) {
System.out.print(findParent(i) + " ");
}
System.out.println();
// 부모 테이블 내용 출력하기
System.out.print("부모 테이블: ");
for (int i = 1; i <= V; i++) {
System.out.print(parent[i] + " ");
}
System.out.println();
}
}
- 위의 소스코드는 최악의 경우 부모 노드를 확인하는 데 모든 노드를 확인할 수도 있다.
아래의 표 처럼 5번 노드의 루트 노드를 확인하는데 4>3>2>1>1을 확인하게 된다.
| 노드 번호 | 1 | 2 | 3 | 4 | 5 |
| 부모 노드 번호 | 1 | 1 | 2 | 3 | 4 |
- 위의 경우 경로 압축 기법을 적용하여 시간 복잡도를 개선시킬 수 있다.
2) 경로 압축(path Compression) : find 함수를 재귀적으로 호출한 뒤에 부모 테이블을 갱신하는 기법
- 위의 소스코드에서 findParent 함수를 아래 코드와 같이 수정하여 경로압축 기법을 사용한다.
public static int findParent(int x) {
// x의 부모노드가 루트노드일 경우 x 반환
if (x == parent[x]){
return x;
}
// 아니면 루트노드 찾은 후에 parent 배열에 넣고 반환
return parent[x] = findParent(parent[x]);
}
3) 서로소 집합을 활용한 사이클 판별
- 서로소 집합은 무방향 그래프 내에서의 사이클을 판별할 때 사용할 수 있다.
- union연산은 그래프에서의 간선으료 표현될 수 있으며, 간선을 하나씩 확인하면서 두 노드가 포함되어 있는 집합을 합치는 과정을 반복하면 사이클 판별 가능
- 각 간선을 확인하며 두 노드의 루트 노드 확인
- 루트 노드가 서로 다르다면 두 노드에 대해 union 연산 진행
- 루트 노드가 서로 같다면 사이클(Cycle)인 것으로 확인
- 그래프에 포함되어 있는 모든 간선에 대하여 1번의 과정 반복
import java.util.*;
public class Main {
// V : 노드의 갯수
// M : 간선의 갯수
public static int V, M;
public static int[] parent = new int[100001]; // 부모 테이블 초기화하기
// 특정 원소가 속한 집합을 찾기
public static int findParent(int x) {
// x가 루트노드 일 경우 x 반환
if (x == parent[x]) {
return x;
}
// 아닐 경우, 루트노드를 찾기위해 재귀 호출 후 이 값을 반환 및 parent 배열에 저장
return parent[x] = findParent(parent[x]);
}
// 두 원소가 속한 집합을 합치기
public static void unionParent(int a, int b) {
a = findParent(a);
b = findParent(b);
if (a < b) parent[b] = a;
else parent[a] = b;
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
V = sc.nextInt();
M = sc.nextInt();
// 부모 테이블상에서, 부모를 자기 자신으로 초기화
for (int i = 1; i <= V; i++) {
parent[i] = i;
}
boolean cycle = false; // 사이클 발생 여부
for (int i = 0; i < M; i++) {
int a = sc.nextInt();
int b = sc.nextInt();
// 사이클이 발생한 경우 종료
if (findParent(a) == findParent(b)) {
cycle = true;
break;
}
// 사이클이 발생하지 않았다면 합집합(Union) 연산 수행
else {
unionParent(a, b);
}
}
if (cycle) {
System.out.println("사이클 있음");
}
else {
System.out.println("사이클 없음");
}
}
}| 입력 | 출력 |
| 3 3 1 2 2 1 2 3 |
사이클 있음 |
3. 신장 트리
1) 신장 트리(Spanning Tree)
- 하나의 그래프가 있을 때 모든 노드를 포함하면서 사이클이 존재하지 않는 부분 그래프
2) 크루스칼 알고리즘(Kruskal Algorithm)
- 신장 트리 중에서 최소 비용으로 만들 수 있는 트리를 찾는 알고리즘 (최소 신장 트리 알고리즘)
- 그리디 알고리즘으로 분류
- 가장 거리가 짧은 간선부터 차례대로 집합에 추가하는 방식
- 간선의 갯수 = 노드의 갯수 -1

ex) 위의 A, B, C 가 모두 연결되기 위한 최소의 비용(최소 신장 트리)은 아래와 같다.
▶ 2+3 (최소 비용)
▶ 3+5
▶ 2+5

3) 크루스칼 알고리즘 동작 과정
- 간선 데이터를 비용에 따라 오름차순 정렬
- 간선을 하나씩 확인하며 현재의 간선이 사이클을 발생시키는 지 확인
- 사이클 발생 시, 최소 신장 트리에 포함 X
- 사이클 발생 하지 않는 경우, 최소 신장 트리에 포함
- 모든 간선에 대하여 2번 과정을 반복
import java.util.ArrayList;
import java.util.Collections;
import java.util.Scanner;
public class Main {
// Edge 클래스 선언
public static class Edge implements Comparable<Edge>{
private int nodeA;
private int nodeB;
private int distance;
public Edge(int nodeA, int nodeB, int distance) {
this.nodeA = nodeA;
this.nodeB = nodeB;
this.distance = distance;
}
public int getNodeA() {
return nodeA;
}
public int getNodeB() {
return nodeB;
}
public int getDistance() {
return distance;
}
// 우선순위 큐에서 사용
// 거리가 낮을 수록 높은 우선순위를 가짐
@Override
public int compareTo(Edge other) {
if(this.distance < other.distance)
return -1;
else
return 1;
}
}
// V : 노드의 갯수(최대 100000개로 가정)
// M : 간선의 갯수
public static int V, M;
// 부모 테이블
public static int[] parent = new int[100001];
// 그래프를 저장할 변수
public static ArrayList<Edge> graph = new ArrayList<>();
// 결과를 저장할 변수
public static int result = 0;
// 특정 원소의 루트 노드 찾기
public static int findParent(int x) {
// x가 루트노드라면 반환
if (x == parent[x])
return x;
// 아니라면 parent[x]가 루트노드가 될 때까지 재귀호출
return parent[x] = findParent(parent[x]);
}
// 두 원소가 속한 루트 노드를 합치기
public static void unionParent(int a, int b) {
a = findParent(a);
b = findParent(b);
// 큰 수가 작은 수를 바라보도록
if (a < b)
parent[b] = a;
else parent[a] = b;
}
public static void main(String[] args) {
// TODO Auto-generated method stub
Scanner sc = new Scanner(System.in);
V = sc.nextInt();
M = sc.nextInt();
// 부모 테이블에서, 부모를 자기 자신으로 초기화
// 0번 노드는 없다고 가정
for (int i = 1; i <= V; i++) {
parent[i] = i;
}
// 모든 간선에 대한 정보를 입력 받기
for (int i = 0; i < M; i++) {
int a = sc.nextInt();
int b = sc.nextInt();
int cost = sc.nextInt();
graph.add(new Edge(a, b, cost));
}
// 간선을 비용순으로 정렬
Collections.sort(graph);
// 간선을 하나씩 확인하며
for (int i = 0; i < graph.size(); i++) {
int cost = graph.get(i).getDistance();
int a = graph.get(i).getNodeA();
int b = graph.get(i).getNodeB();
// 사이클이 발생하지 않는 경우에만 최소 신장 트리에 포함
// 사이클이 발생하지 않는다 = a와 b의 루트 노드가 같지 않다
if (findParent(a) != findParent(b)) {
unionParent(a, b);
result += cost;
}
}
// 결과 출력
System.out.println(result);
}
}
4. 위상 정렬
1) 위상 정렬(Topology Sort) : 순서가 정해져 있는 일련의 작업을 차례대로 수행해야 사용할 수 있는 알고리즘
- 방향 그래프의 모든 노드를 '방향성에 거스르지 않도록 순서대로 나열하는 것'
- 진입차수(Indegree) : 특정한 노드로 들어오는 간선의 개수
2) 위상 정렬의 동작 과정
- 진입차수가 0인 노드를 큐에 넣는다.
- 큐가 빌 때까지 아래의 과정을 반복한다.
- 큐에서 원소를 꺼내 해당 노드에서 출발하는 간선을 그래프에서 제거한다.
- 새롭게 진입차수가 0이 된 노드를 큐에 넣는다.
- 만약, 모든 원소를 방문하기 전에 큐가 비어버리면 사이클이 발생한 것이다. (위상 정렬 문제에서는 사이클이 존재하지 않는다고 명시하는 경우가 많음)
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.Queue;
import java.util.StringTokenizer;
public class Main {
// N : 노드의 갯수
// M : 간선의 갯수
public static int N, M;
// 그래프
public static ArrayList<ArrayList<Integer>> graph = new ArrayList<ArrayList<Integer>>();
// 각 노드 별 진입차수 체크
public static int[] inde;
public static void topologySort() {
Queue<Integer> q = new LinkedList<>();
ArrayList<Integer> result = new ArrayList<>();
// 진입차수가 0인 노드를 큐에 넣기
for(int i=1; i<=N; i++) {
if(inde[i]==0)
q.offer(i);
}
// 큐가 빌 때까지 반복
while(!q.isEmpty()) {
// 큐에서 꺼내고
int now = q.poll();
// 결과 리스트에 넣기
result.add(now);
// 현재 큐에서 이어지는 간선을 빼주기
for(int i=0; i<graph.get(now).size(); i++) {
inde[graph.get(now).get(i)] -= 1;
// 그 때, 진입차수가 0이면 큐에 넣기
if(inde[graph.get(now).get(i)] == 0)
q.offer(graph.get(now).get(i));
}
}
System.out.print("순서 : ");
// 결과 출력
for(int i=0;i<result.size();i++) {
System.out.print(result.get(i)+" ");
}
}
public static void main(String[] args) throws IOException {
// TODO Auto-generated method stub
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
// 노드의 갯수와 간선의 갯수 입력받기
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
// 진입차수 배열 크기 할당
inde = new int[N+1];
// 그래프 설정
for(int i=0;i<N+1; i++) {
graph.add(new ArrayList<Integer>());
}
for(int i=0; i<M; i++) {
st = new StringTokenizer(br.readLine());
int from = Integer.parseInt(st.nextToken());
int to = Integer.parseInt(st.nextToken());
graph.get(from).add(to);
// 진입차수 설정
inde[to] += 1;
}
// 위상정렬 호출
topologySort();
}
}| 입력 | 출력 |
| 7 8 1 2 1 5 2 3 2 6 3 4 4 7 5 6 6 4 |
순서 : 1 2 5 3 6 4 7 |
'Algorithm' 카테고리의 다른 글
| [이것이 코딩테스트다] 9. 그래프 - 실전 문제 풀이 (0) | 2022.02.12 |
|---|---|
| [BAEKJOON] 2665번 : 미로만들기 (JAVA) (0) | 2022.02.11 |
| [BAEKJOON] 4485번 : 녹색 옷 입은 애가 젤다지? (JAVA) (0) | 2022.02.08 |
| [BAEKJOON] 13549번 : 숨바꼭질 3 (JAVA) (0) | 2022.02.07 |
| [BAEKJOON] 1916번 : 최소 비용 구하기 (JAVA) (0) | 2022.02.04 |
