
이 포스팅에서 작성하는 내용은 이것이 취업을 위한 코딩테스트다 (나동빈 지음) 에서 발췌하였습니다.
그래프
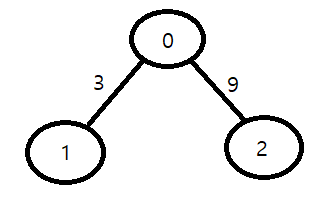
- 구성 : 노드(정점), 간선
- A노드와 B노드가 간선으로 연결되어 있는 경우 'A노드와 B노드는 인접하다.' 라고 표현
프로그래밍에서의 그래프 표현 방법
# 인접 행렬 : 2차원 배열로 그래프의 연결 관계 표현
- 2차원 배열에 각 노드가 연결된 형태를 기록
- 간선으로 연결되어 있지 않은 노드는 '무한' or '99999999' 와 같은 정답이 될 수 없는 큰 값으로 초기화 하는 경우가 多
public class Main {
public static final int INFINITE = 999999999;
// 2차원 배열를 이용해 인접 행렬 표현
public static int[][] graph = {
{0, 3, 9},
{3, 0, INFINITE},
{9, INFINITE, 0}
};
public static void main(String[] args) {
// 그래프 출력
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 3; j++) {
System.out.print(graph[i][j] + " ");
}
System.out.println();
}
}
}| 0 3 9 3 0 999999999 9 999999999 0 |
# 인접 리스트 : 리스트로 그래프의 연결 관계 표현
- '연결 리스트' 라는 자료구조를 이용해 모든 노드에 연결된 노드에 대한 정보를 이어 저장
- C++ / JAVA : 별도로 연결 리스트 기능을 위한 표준 라이브러리 제공
- Python : 기본 자료형인 리스트에서 append()와 메소드를 제공
import java.util.*;
public class Main {
// 인접 리스트 선언
public static ArrayList<ArrayList<Node>> graph = new ArrayList<ArrayList<Node>>();
public static void main(String[] args) {
// 그래프에 3개의 노드 추가
for (int i = 0; i < 3; i++) {
graph.add(new ArrayList<Node>());
}
// 노드 0에서 다른 노드와 연결된 노드 정보 저장 (노드, 거리)
graph.get(0).add(new Node(1, 3));
graph.get(0).add(new Node(2, 9));
// 노드 1에서 다른 노드와 연결된 노드 정보 저장 (노드, 거리)
graph.get(1).add(new Node(0, 3));
// 노드 2에서 다른 노드와 연결된 노드 정보 저장 (노드, 거리)
graph.get(2).add(new Node(0, 9));
// 그래프 출력
for (int i = 0; i < graph.size(); i++) {
System.out.print(" (FROM : " + i + ") -> ");
for (int j = 0; j < graph.get(i).size(); j++) {
graph.get(i).get(j).print();
}
System.out.println();
}
}
// 노드 클래스 선언
static class Node {
private int index;
private int distance;
// 생성자로 클래스의 변수 초기화
public Node(int index, int distance) {
this.index = index;
this.distance = distance;
}
// 출력
public void print() {
System.out.print("[To : " + this.index + ", Distance : " + this.distance + "] ");
}
}
}| (FROM : 0) -> [To : 1, Distance : 3] [To : 2, Distance : 9] (FROM : 1) -> [To : 0, Distance : 3] (FROM : 2) -> [To : 0, Distance : 9] |
# 인접 행렬 vs 인접 리스트
- 인접 행렬 : 모든 관계를 저장하여 노드의 개수가 많을 경우 메모리 사용량이 높아지지만, 특정 노드의 관계에 대한 정보를 얻는 속도는 빠르다.
- 인접 리스트 : 연결된 정보만을 저장하기 때문에 메모리를 효율적으로 사용하지만, 특정 노드의 관계에 대한 정보를 얻는 속도는 느리다.
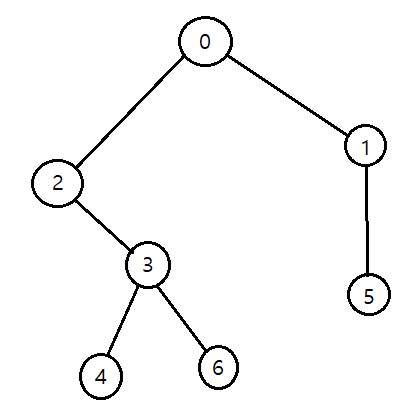
DFS(Depth-First Search) : 깊이 우선 탐색
그래프에서 깊은 부분을 우선적으로 탐색하는 알고리즘이며, 아래 예제에서는 스택과 재귀함수를 이용한다.
import java.util.*;
public class Main {
// 방문했던 노드를 체크하기 위한 변수
public static boolean[] visited_Node = new boolean[7];
// 그래프 변수
public static ArrayList<ArrayList<Integer>> graph = new ArrayList<ArrayList<Integer>>();
// DFS 함수
// 깊이우선탐색
// 같은 Depth가 있을 경우, 작은 숫자를 먼저 방문(add를 작은 숫자 먼저 했기 때문)
public static void dfs(int num) {
// 현재 노드를 방문 처리
visited_Node[num] = true;
System.out.print(num + " ");
// 현재 노드와 연결된 다른 노드를 재귀적으로 방문
for (int i = 0; i < graph.get(num).size(); i++) {
int temp = graph.get(num).get(i);
if (!visited_Node[temp])
dfs(temp);
}
}
public static void main(String[] args) {
// 그래프에 7개의 노드 추가
for (int i = 0; i < 7; i++) {
graph.add(new ArrayList<Integer>());
}
// 노드 0에 연결된 노드 정보 저장
graph.get(0).add(1);
graph.get(0).add(2);
// 노드 1에 연결된 노드 정보 저장
graph.get(1).add(0);
graph.get(1).add(5);
// 노드 2에 연결된 노드 정보 저장
graph.get(2).add(0);
graph.get(2).add(3);
// 노드 3에 연결된 노드 정보 저장
graph.get(3).add(2);
graph.get(3).add(4);
graph.get(3).add(6);
// 노드 4에 연결된 노드 정보 저장
graph.get(4).add(3);
// 노드 5에 연결된 노드 정보 저장
graph.get(5).add(1);
// 노드 6에 연결된 노드 정보 저장
graph.get(6).add(3);
dfs(0);
}
}| 0 1 5 2 3 4 6 |
BFS(Breadth-First Search) : 너비 우선 탐색
그래프에서 가까운 노드부터 탐색하는 알고리즘이며, 아래 예제에서는 선입선출의 특성을 가진 큐(Queue)를 이용한다.
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.Queue;
public class Main {
// 방문했던 노드를 체크하기 위한 변수
public static boolean[] visited_Node = new boolean[7];
// 그래프 변수
public static ArrayList<ArrayList<Integer>> graph = new ArrayList<ArrayList<Integer>>();
// BFS 함수
// 너비우선탐색
// 가까이 있는 원소부터 탐색
public static void bfs(int num) {
Queue<Integer> queue = new LinkedList<>();
queue.offer(num);
// 현재 노드를 방문 처리
visited_Node[num] = true;
// queue가 빌 때까지 반복
while(!queue.isEmpty()) {
// queue에서 하나의 원소를 뽑음
// 선입선출이기에 먼저 들어온 것이 먼저 뽑힘
int x = queue.poll();
System.out.print(x + " ");
// 해당 원소와 연결되어 있는 원소 확인
for(int i = 0; i < graph.get(x).size(); i++) {
int y = graph.get(x).get(i);
// 아직 방문처리가 안 된 원소는 queue에 넣고 방문 처리
if(!visited_Node[y]) {
queue.offer(y);
visited_Node[y] = true;
}
}
}
}
public static void main(String[] args) {
// 그래프에 7개의 노드 추가
for (int i = 0; i < 7; i++) {
graph.add(new ArrayList<Integer>());
}
// 노드 0에 연결된 노드 정보 저장
graph.get(0).add(1);
graph.get(0).add(2);
// 노드 1에 연결된 노드 정보 저장
graph.get(1).add(0);
graph.get(1).add(5);
// 노드 2에 연결된 노드 정보 저장
graph.get(2).add(0);
graph.get(2).add(3);
// 노드 3에 연결된 노드 정보 저장
graph.get(3).add(2);
graph.get(3).add(4);
graph.get(3).add(6);
// 노드 4에 연결된 노드 정보 저장
graph.get(4).add(3);
// 노드 5에 연결된 노드 정보 저장
graph.get(5).add(1);
// 노드 6에 연결된 노드 정보 저장
graph.get(6).add(3);
bfs(0);
}
}| 0 1 2 5 3 4 6 |
응용 문제
1. 음료수 얼려먹기
DFS를 이용하여 문제 해결
import java.util.ArrayList;
import java.util.Scanner;
public class Main {
public static int x,y;
// 방문했던 노드를 체크하기 위한 변수
public static boolean[] visited_Node = new boolean[1000000];
// 그래프 변수
public static int[][] graph = new int[1000][1000];
public static boolean dfs(int temp_y, int temp_x) {
// 범위가 벗어나는 경우 종료
if(temp_y < 0 || temp_y >= y || temp_x < 0 || temp_x >= x) {
return false;
}
if(graph[temp_y][temp_x] == 0) {
// 방문 안 한 경우
graph[temp_y][temp_x] = 1; // 방문 처리
// dfs 재귀함수를 이용하는 이유? 상하좌우가 붙어있는 경우 하나로 간주하기 때문에 dfs 재귀함수를 이용해서 방문했었다. 를 기록하기 위함임.
// 위의 '방문했었다.' 란 뜻은 이 노드는 이제 신경쓰지마라 라는 걸로 이해할 수 있음
// 아래는 상하좌우를 체크하는 것
dfs(temp_y+1,temp_x);
dfs(temp_y-1,temp_x);
dfs(temp_y,temp_x+1);
dfs(temp_y,temp_x-1);
return true;
}
else {
// 이미 방문 한 경우 반환
return false;
}
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
y = sc.nextInt();
x = sc.nextInt();
// 버퍼 지우기
sc.nextLine();
// 음료수의 갯수
int result = 0;
// String.charAt(i) : 문자열에서 해당 위치의 문자를 가져오는 함수
// 주의점 : char 타입으로 리턴된다. -> 즉, 아래의 int 타입으로 데이터를 넣으려고 할 땐 - '0'이 필요하다.
for(int i=0;i<y;i++) {
String temp = sc.nextLine();
for(int j=0;j<x;j++) {
graph[i][j] = temp.charAt(j)-'0';
}
}
// DFS 알고리즘을 이용하여 음료수의 갯수를 확인한다.
for(int i=0;i<y;i++) {
for(int j=0;j<x;j++) {
if(dfs(i,j)) {
result++;
};
}
}
// 결과 출력
System.out.println(result);
}
}
2. 미로 탈출
Node와 BFS를 이용하여 문제 해결
import java.util.LinkedList;
import java.util.Queue;
import java.util.Scanner;
// 노드 클래스 정의
class Node{
private int num1;
private int num2;
// 생성자를 이용하여 변수 할당
public Node(int num1, int num2) {
this.num1 = num1;
this.num2 = num2;
}
public int getNum1() {
return this.num1;
}
public int getNum2() {
return this.num2;
}
}
public class Main {
public static int num1,num2;
public static int[][] graph = new int[200][200];
// 이동할 네 가지 방향 정의 (상, 하, 좌, 우)
public static int dnum1[] = {-1, 1, 0, 0};
public static int dnum2[] = {0, 0, -1, 1};
public static int bfs(int temp_num1, int temp_num2) {
// queue.offer() : 삽입
// queue.poll() : 빼고 확인
Queue<Node> queue = new LinkedList<>();
queue.offer(new Node(temp_num1, temp_num2));
// 큐가 빌 때 까지
while(!queue.isEmpty()) {
Node node = queue.poll();
temp_num1 = node.getNum1();
temp_num2 = node.getNum2();
// 상하좌우 체크
for(int i=0;i<dnum1.length;i++) {
int nNum1 = temp_num1 + dnum1[i];
int nNum2 = temp_num2 + dnum2[i];
if(nNum1 >= num1 || nNum1 < 0 || nNum2 >= num2 || nNum2 < 0) {
continue;
}
else {
int temp = graph[nNum1][nNum2];
if(temp == 0) {
continue;
}
// 방문 안한 노드의 경우 이전 노드의 +1 처리 후 큐에 삽입
else if(temp == 1) {
graph[nNum1][nNum2] = graph[temp_num1][temp_num2]+1;
queue.offer(new Node(nNum1,nNum2));
}
}
}
}
return graph[num1-1][num2-1];
}
public static void main(String[] args) {
// TODO Auto-generated method stub
Scanner sc = new Scanner(System.in);
num1 = sc.nextInt();
num2 = sc.nextInt();
sc.nextLine(); // remove buffer
// String.charAt(i) : 문자열에서 해당 위치의 문자를 가져오는 함수
// 주의점 : char 타입으로 리턴된다. -> 즉, 아래의 int 타입으로 데이터를 넣으려고 할 땐 - '0'이 필요하다.
for(int i=0;i<num1;i++) {
String temp = sc.nextLine();
for(int j=0;j<num2;j++) {
graph[i][j] = temp.charAt(j) - '0';
}
}
System.out.println(bfs(0,0));
}
}'Algorithm' 카테고리의 다른 글
| [BAEKJOON] 2178번 : 미로탐색 (0) | 2022.01.06 |
|---|---|
| [BAEKJOON] 1260번 : DFS와 BFS (0) | 2022.01.03 |
| [이것이 코딩테스트다] 4. DFS/BFS - Stack, Queue, 재귀함수 (0) | 2021.12.24 |
| [BAEKJOON] 2869번 : 달팽이는 올라가고 싶다 (0) | 2021.12.22 |
| [이것이 코딩테스트다] 2. 그리디(Greedy) 알고리즘 (0) | 2021.12.13 |

이 포스팅에서 작성하는 내용은 이것이 취업을 위한 코딩테스트다 (나동빈 지음) 에서 발췌하였습니다.
그래프

- 구성 : 노드(정점), 간선
- A노드와 B노드가 간선으로 연결되어 있는 경우 'A노드와 B노드는 인접하다.' 라고 표현
프로그래밍에서의 그래프 표현 방법
# 인접 행렬 : 2차원 배열로 그래프의 연결 관계 표현
- 2차원 배열에 각 노드가 연결된 형태를 기록
- 간선으로 연결되어 있지 않은 노드는 '무한' or '99999999' 와 같은 정답이 될 수 없는 큰 값으로 초기화 하는 경우가 多
public class Main {
public static final int INFINITE = 999999999;
// 2차원 배열를 이용해 인접 행렬 표현
public static int[][] graph = {
{0, 3, 9},
{3, 0, INFINITE},
{9, INFINITE, 0}
};
public static void main(String[] args) {
// 그래프 출력
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 3; j++) {
System.out.print(graph[i][j] + " ");
}
System.out.println();
}
}
}| 0 3 9 3 0 999999999 9 999999999 0 |
# 인접 리스트 : 리스트로 그래프의 연결 관계 표현
- '연결 리스트' 라는 자료구조를 이용해 모든 노드에 연결된 노드에 대한 정보를 이어 저장
- C++ / JAVA : 별도로 연결 리스트 기능을 위한 표준 라이브러리 제공
- Python : 기본 자료형인 리스트에서 append()와 메소드를 제공
import java.util.*;
public class Main {
// 인접 리스트 선언
public static ArrayList<ArrayList<Node>> graph = new ArrayList<ArrayList<Node>>();
public static void main(String[] args) {
// 그래프에 3개의 노드 추가
for (int i = 0; i < 3; i++) {
graph.add(new ArrayList<Node>());
}
// 노드 0에서 다른 노드와 연결된 노드 정보 저장 (노드, 거리)
graph.get(0).add(new Node(1, 3));
graph.get(0).add(new Node(2, 9));
// 노드 1에서 다른 노드와 연결된 노드 정보 저장 (노드, 거리)
graph.get(1).add(new Node(0, 3));
// 노드 2에서 다른 노드와 연결된 노드 정보 저장 (노드, 거리)
graph.get(2).add(new Node(0, 9));
// 그래프 출력
for (int i = 0; i < graph.size(); i++) {
System.out.print(" (FROM : " + i + ") -> ");
for (int j = 0; j < graph.get(i).size(); j++) {
graph.get(i).get(j).print();
}
System.out.println();
}
}
// 노드 클래스 선언
static class Node {
private int index;
private int distance;
// 생성자로 클래스의 변수 초기화
public Node(int index, int distance) {
this.index = index;
this.distance = distance;
}
// 출력
public void print() {
System.out.print("[To : " + this.index + ", Distance : " + this.distance + "] ");
}
}
}| (FROM : 0) -> [To : 1, Distance : 3] [To : 2, Distance : 9] (FROM : 1) -> [To : 0, Distance : 3] (FROM : 2) -> [To : 0, Distance : 9] |
# 인접 행렬 vs 인접 리스트
- 인접 행렬 : 모든 관계를 저장하여 노드의 개수가 많을 경우 메모리 사용량이 높아지지만, 특정 노드의 관계에 대한 정보를 얻는 속도는 빠르다.
- 인접 리스트 : 연결된 정보만을 저장하기 때문에 메모리를 효율적으로 사용하지만, 특정 노드의 관계에 대한 정보를 얻는 속도는 느리다.

DFS(Depth-First Search) : 깊이 우선 탐색
그래프에서 깊은 부분을 우선적으로 탐색하는 알고리즘이며, 아래 예제에서는 스택과 재귀함수를 이용한다.
import java.util.*;
public class Main {
// 방문했던 노드를 체크하기 위한 변수
public static boolean[] visited_Node = new boolean[7];
// 그래프 변수
public static ArrayList<ArrayList<Integer>> graph = new ArrayList<ArrayList<Integer>>();
// DFS 함수
// 깊이우선탐색
// 같은 Depth가 있을 경우, 작은 숫자를 먼저 방문(add를 작은 숫자 먼저 했기 때문)
public static void dfs(int num) {
// 현재 노드를 방문 처리
visited_Node[num] = true;
System.out.print(num + " ");
// 현재 노드와 연결된 다른 노드를 재귀적으로 방문
for (int i = 0; i < graph.get(num).size(); i++) {
int temp = graph.get(num).get(i);
if (!visited_Node[temp])
dfs(temp);
}
}
public static void main(String[] args) {
// 그래프에 7개의 노드 추가
for (int i = 0; i < 7; i++) {
graph.add(new ArrayList<Integer>());
}
// 노드 0에 연결된 노드 정보 저장
graph.get(0).add(1);
graph.get(0).add(2);
// 노드 1에 연결된 노드 정보 저장
graph.get(1).add(0);
graph.get(1).add(5);
// 노드 2에 연결된 노드 정보 저장
graph.get(2).add(0);
graph.get(2).add(3);
// 노드 3에 연결된 노드 정보 저장
graph.get(3).add(2);
graph.get(3).add(4);
graph.get(3).add(6);
// 노드 4에 연결된 노드 정보 저장
graph.get(4).add(3);
// 노드 5에 연결된 노드 정보 저장
graph.get(5).add(1);
// 노드 6에 연결된 노드 정보 저장
graph.get(6).add(3);
dfs(0);
}
}| 0 1 5 2 3 4 6 |
BFS(Breadth-First Search) : 너비 우선 탐색
그래프에서 가까운 노드부터 탐색하는 알고리즘이며, 아래 예제에서는 선입선출의 특성을 가진 큐(Queue)를 이용한다.
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.Queue;
public class Main {
// 방문했던 노드를 체크하기 위한 변수
public static boolean[] visited_Node = new boolean[7];
// 그래프 변수
public static ArrayList<ArrayList<Integer>> graph = new ArrayList<ArrayList<Integer>>();
// BFS 함수
// 너비우선탐색
// 가까이 있는 원소부터 탐색
public static void bfs(int num) {
Queue<Integer> queue = new LinkedList<>();
queue.offer(num);
// 현재 노드를 방문 처리
visited_Node[num] = true;
// queue가 빌 때까지 반복
while(!queue.isEmpty()) {
// queue에서 하나의 원소를 뽑음
// 선입선출이기에 먼저 들어온 것이 먼저 뽑힘
int x = queue.poll();
System.out.print(x + " ");
// 해당 원소와 연결되어 있는 원소 확인
for(int i = 0; i < graph.get(x).size(); i++) {
int y = graph.get(x).get(i);
// 아직 방문처리가 안 된 원소는 queue에 넣고 방문 처리
if(!visited_Node[y]) {
queue.offer(y);
visited_Node[y] = true;
}
}
}
}
public static void main(String[] args) {
// 그래프에 7개의 노드 추가
for (int i = 0; i < 7; i++) {
graph.add(new ArrayList<Integer>());
}
// 노드 0에 연결된 노드 정보 저장
graph.get(0).add(1);
graph.get(0).add(2);
// 노드 1에 연결된 노드 정보 저장
graph.get(1).add(0);
graph.get(1).add(5);
// 노드 2에 연결된 노드 정보 저장
graph.get(2).add(0);
graph.get(2).add(3);
// 노드 3에 연결된 노드 정보 저장
graph.get(3).add(2);
graph.get(3).add(4);
graph.get(3).add(6);
// 노드 4에 연결된 노드 정보 저장
graph.get(4).add(3);
// 노드 5에 연결된 노드 정보 저장
graph.get(5).add(1);
// 노드 6에 연결된 노드 정보 저장
graph.get(6).add(3);
bfs(0);
}
}| 0 1 2 5 3 4 6 |
응용 문제
1. 음료수 얼려먹기
DFS를 이용하여 문제 해결
import java.util.ArrayList;
import java.util.Scanner;
public class Main {
public static int x,y;
// 방문했던 노드를 체크하기 위한 변수
public static boolean[] visited_Node = new boolean[1000000];
// 그래프 변수
public static int[][] graph = new int[1000][1000];
public static boolean dfs(int temp_y, int temp_x) {
// 범위가 벗어나는 경우 종료
if(temp_y < 0 || temp_y >= y || temp_x < 0 || temp_x >= x) {
return false;
}
if(graph[temp_y][temp_x] == 0) {
// 방문 안 한 경우
graph[temp_y][temp_x] = 1; // 방문 처리
// dfs 재귀함수를 이용하는 이유? 상하좌우가 붙어있는 경우 하나로 간주하기 때문에 dfs 재귀함수를 이용해서 방문했었다. 를 기록하기 위함임.
// 위의 '방문했었다.' 란 뜻은 이 노드는 이제 신경쓰지마라 라는 걸로 이해할 수 있음
// 아래는 상하좌우를 체크하는 것
dfs(temp_y+1,temp_x);
dfs(temp_y-1,temp_x);
dfs(temp_y,temp_x+1);
dfs(temp_y,temp_x-1);
return true;
}
else {
// 이미 방문 한 경우 반환
return false;
}
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
y = sc.nextInt();
x = sc.nextInt();
// 버퍼 지우기
sc.nextLine();
// 음료수의 갯수
int result = 0;
// String.charAt(i) : 문자열에서 해당 위치의 문자를 가져오는 함수
// 주의점 : char 타입으로 리턴된다. -> 즉, 아래의 int 타입으로 데이터를 넣으려고 할 땐 - '0'이 필요하다.
for(int i=0;i<y;i++) {
String temp = sc.nextLine();
for(int j=0;j<x;j++) {
graph[i][j] = temp.charAt(j)-'0';
}
}
// DFS 알고리즘을 이용하여 음료수의 갯수를 확인한다.
for(int i=0;i<y;i++) {
for(int j=0;j<x;j++) {
if(dfs(i,j)) {
result++;
};
}
}
// 결과 출력
System.out.println(result);
}
}
2. 미로 탈출
Node와 BFS를 이용하여 문제 해결
import java.util.LinkedList;
import java.util.Queue;
import java.util.Scanner;
// 노드 클래스 정의
class Node{
private int num1;
private int num2;
// 생성자를 이용하여 변수 할당
public Node(int num1, int num2) {
this.num1 = num1;
this.num2 = num2;
}
public int getNum1() {
return this.num1;
}
public int getNum2() {
return this.num2;
}
}
public class Main {
public static int num1,num2;
public static int[][] graph = new int[200][200];
// 이동할 네 가지 방향 정의 (상, 하, 좌, 우)
public static int dnum1[] = {-1, 1, 0, 0};
public static int dnum2[] = {0, 0, -1, 1};
public static int bfs(int temp_num1, int temp_num2) {
// queue.offer() : 삽입
// queue.poll() : 빼고 확인
Queue<Node> queue = new LinkedList<>();
queue.offer(new Node(temp_num1, temp_num2));
// 큐가 빌 때 까지
while(!queue.isEmpty()) {
Node node = queue.poll();
temp_num1 = node.getNum1();
temp_num2 = node.getNum2();
// 상하좌우 체크
for(int i=0;i<dnum1.length;i++) {
int nNum1 = temp_num1 + dnum1[i];
int nNum2 = temp_num2 + dnum2[i];
if(nNum1 >= num1 || nNum1 < 0 || nNum2 >= num2 || nNum2 < 0) {
continue;
}
else {
int temp = graph[nNum1][nNum2];
if(temp == 0) {
continue;
}
// 방문 안한 노드의 경우 이전 노드의 +1 처리 후 큐에 삽입
else if(temp == 1) {
graph[nNum1][nNum2] = graph[temp_num1][temp_num2]+1;
queue.offer(new Node(nNum1,nNum2));
}
}
}
}
return graph[num1-1][num2-1];
}
public static void main(String[] args) {
// TODO Auto-generated method stub
Scanner sc = new Scanner(System.in);
num1 = sc.nextInt();
num2 = sc.nextInt();
sc.nextLine(); // remove buffer
// String.charAt(i) : 문자열에서 해당 위치의 문자를 가져오는 함수
// 주의점 : char 타입으로 리턴된다. -> 즉, 아래의 int 타입으로 데이터를 넣으려고 할 땐 - '0'이 필요하다.
for(int i=0;i<num1;i++) {
String temp = sc.nextLine();
for(int j=0;j<num2;j++) {
graph[i][j] = temp.charAt(j) - '0';
}
}
System.out.println(bfs(0,0));
}
}'Algorithm' 카테고리의 다른 글
| [BAEKJOON] 2178번 : 미로탐색 (0) | 2022.01.06 |
|---|---|
| [BAEKJOON] 1260번 : DFS와 BFS (0) | 2022.01.03 |
| [이것이 코딩테스트다] 4. DFS/BFS - Stack, Queue, 재귀함수 (0) | 2021.12.24 |
| [BAEKJOON] 2869번 : 달팽이는 올라가고 싶다 (0) | 2021.12.22 |
| [이것이 코딩테스트다] 2. 그리디(Greedy) 알고리즘 (0) | 2021.12.13 |
